اعداد روندا(Rhonda)
در اين مقاله به معرفي اعداد روندا(Rhonda) و ذكر نمونه هايي از آن پرداخته و ... |
 |
|
تعريف:عدد طبيعي n يك عدد روندا در مبناي B (عدد طبيعي) ناميده ميشود اگر حاصلضرب ارقام n در مبناي Bمساوي B برابر مجموع عوامل اول n باشد.نتيجه ي فوري از تعريف اين است كه اگر n در مبناي B روندا باشد،تمامي ارقام n در مبناي B غير صفرند. مثال: 25662 يك عدد روندا در مبناي 10 است،نمايش آن به صورت حاصل ضرب عوامل اول چنين است: 47 × 13 × 7 × 3 × 2 = 25662 و هم چنين داريم: (47+13+7+3+2)×10 = 2×6×6×5×2.
نكته:براي مبناهايي كه عدد اول هستند،عدد روندايي وجود ندارد،چرا كه براي عدد اول دلخواه p،p هيچ حاصل ضربي از اعداد طبيعي كوچك تر از خود را عاد نمي كند. در جدول زير چند عدد روندا در مبناهاي ذكر شده را آورده ايم:
عدد 560 كوچك ترين عدد روندا است كه در مبناي 12 روندا ميباشد(توجه كنيد كه ارقام 560 در مبناي 12 عبارت هستند از:8و10و3)؛اعدادي طبيعي وجود دارند كه براي بيش از يك مبنا،روندا هستند. مثلاً عدد 1000 كوچك ترين اين اعداد است كه براي مبناهاي 16 و 36 روندا است. تعريف:براي عدد طبيعي n، توجه كنيد كه چون براي هر n، مثال: اگر در روابط فوق، 6=m قرار دهيم آن گاه از: 4= 13×2-7-5-7×6 = داريم: 4=k و لذا نمايش N در مبناي B به صورت زير است: حاصل ضرب ارقام N در مبناي B برابر است با: بنابراين B برابر مجموع عوامل اول N مساوي است با اين بحث نشان مي دهد كه اعداد روندا نامتناهي هستند.
|


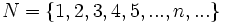 با کمی دقت متوجه میشویم که میتوان یک
با کمی دقت متوجه میشویم که میتوان یک 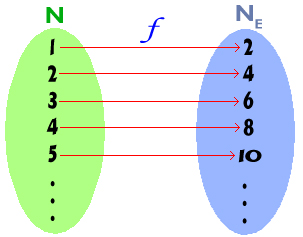
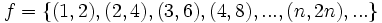 متوجه میشویم
متوجه میشویم 
 را در نظر بگیرید. بیاید بجای اینکه به جای متغیر تابع عددی حقیقی قرار دهیم، متغیرهای طبیعی را جایگزین کنیم. در این صورت داریم:
را در نظر بگیرید. بیاید بجای اینکه به جای متغیر تابع عددی حقیقی قرار دهیم، متغیرهای طبیعی را جایگزین کنیم. در این صورت داریم: 
 ،
،  ، که در آنها n عددی طبیعی است.
، که در آنها n عددی طبیعی است. 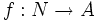
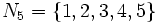 است و دنباله اعداد زوج دنبالهای نامتناهی است چرا که دامنه آن خود مجموعه اعداد طبیعی است.
است و دنباله اعداد زوج دنبالهای نامتناهی است چرا که دامنه آن خود مجموعه اعداد طبیعی است. 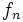 نشان میدهیم. پس برای نمایش مقدار دنباله f به ازای عدد طبیعی n بجای نماد (f(n معمولا از نماد
نشان میدهیم. پس برای نمایش مقدار دنباله f به ازای عدد طبیعی n بجای نماد (f(n معمولا از نماد 
 استفاده میکنیم. پس دنباله اعداد طبیعی زوج را به این صورت نشان می دهیم:
استفاده میکنیم. پس دنباله اعداد طبیعی زوج را به این صورت نشان می دهیم: 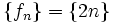
 را یک دنباله حقیقی میگویند.
را یک دنباله حقیقی میگویند.  دنبالهای حقیقی است چرا که برد آن از مجموعه اعداد حقیقی است.
دنبالهای حقیقی است چرا که برد آن از مجموعه اعداد حقیقی است. 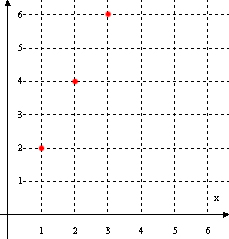

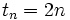 است که همانند
است که همانند 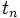 را بدست آورد.
را بدست آورد. 
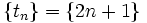
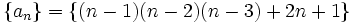

 است ولی از جمله سوم به بعد مانند آن دنباله عمل نمی کند.
است ولی از جمله سوم به بعد مانند آن دنباله عمل نمی کند. 

 را درنظر بگیرید. چند جمله اول این دنباله به این صورت است:
را درنظر بگیرید. چند جمله اول این دنباله به این صورت است: 
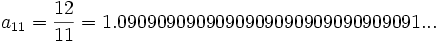





 بدست میآید و اگر n را 1000000000000 انتخاب کنیم مقدار دنباله برابر خواهد بود با عدد
بدست میآید و اگر n را 1000000000000 انتخاب کنیم مقدار دنباله برابر خواهد بود با عدد  که مقداری بسیار نزدیک به 1 است. آیا میتوان با اطمینان گفت با انتخاب n مناسب میتوان بیشتر و بیشتر به 1 نزدیک شد و تقریبهای نزدیکتر به عدد 1 بدست آورد؟
که مقداری بسیار نزدیک به 1 است. آیا میتوان با اطمینان گفت با انتخاب n مناسب میتوان بیشتر و بیشتر به 1 نزدیک شد و تقریبهای نزدیکتر به عدد 1 بدست آورد؟ 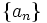 را به هر میزان میتوان به 1 نزدیک کرد به شرط اینکه n به قدر کافی بزرگ انتخاب شده باشد. بیاید با هم سعی در اثبات این حدس کنیم.
را به هر میزان میتوان به 1 نزدیک کرد به شرط اینکه n به قدر کافی بزرگ انتخاب شده باشد. بیاید با هم سعی در اثبات این حدس کنیم.  (که اپسیلون عددی حقیقی مثبت و لخواه است)، بالاخره بهازای یک N ای جملات دنباله
(که اپسیلون عددی حقیقی مثبت و لخواه است)، بالاخره بهازای یک N ای جملات دنباله 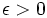 یک N ای از اعداد طبیعی وجود دارد که برای n>N داریم:
یک N ای از اعداد طبیعی وجود دارد که برای n>N داریم:

 را انتخاب کنیم (یعنی اپسیلون را 0.01 بگیریم) برای n>1000 خواهیم داشت:
را انتخاب کنیم (یعنی اپسیلون را 0.01 بگیریم) برای n>1000 خواهیم داشت:  یعنی از جمله 1000ام به بعد همه جملات دنباله در این همسایگی قرار میگیرند. زیرا ، n>1000 و لذا داریم
یعنی از جمله 1000ام به بعد همه جملات دنباله در این همسایگی قرار میگیرند. زیرا ، n>1000 و لذا داریم  و در نتیجه:
و در نتیجه: 



 میتوان نامساوی
میتوان نامساوی  ایجاب میکند
ایجاب میکند  که نماد
که نماد  نماد جزء صحیح است. بوضوح N ای که معرفی کردیم عدی طبیعی است و همچنین بنابر خواص جز صحیح عددی بزرگتر از
نماد جزء صحیح است. بوضوح N ای که معرفی کردیم عدی طبیعی است و همچنین بنابر خواص جز صحیح عددی بزرگتر از  را ایجاب میکند زیرا:
را ایجاب میکند زیرا: 


 بگیریم که در این صورت جملات دنباله از این N به بعد همگی در همسایگی مورد نظر ما قرار میگیرند. و به این ترتیب درستی حدس ما معلوم میشود. در دنباله
بگیریم که در این صورت جملات دنباله از این N به بعد همگی در همسایگی مورد نظر ما قرار میگیرند. و به این ترتیب درستی حدس ما معلوم میشود. در دنباله 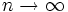 ، آنگاه
، آنگاه  و یا به طور سادهتر
و یا به طور سادهتر  .
. 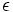 ، عددی طبیعی چون
، عددی طبیعی چون  موجود باشد که برای هر n>N داشته باشیم:
موجود باشد که برای هر n>N داشته باشیم: 

 یا
یا  . به بیان سادهتر و کمی دورتر از عبارات صوری ریاضی، L حد دنباله
. به بیان سادهتر و کمی دورتر از عبارات صوری ریاضی، L حد دنباله 

 و یک بینهایت بزرگ میگوییم هرگاه
و یک بینهایت بزرگ میگوییم هرگاه 


 از اینجا داریم:
از اینجا داریم: 




 اختیار کنیم مثلاً
اختیار کنیم مثلاً  حال ادعا میکنیم این همان m ای است که برای هر n>m داریم:
حال ادعا میکنیم این همان m ای است که برای هر n>m داریم: 
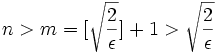


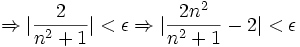
 واگرا است.
واگرا است.  و
و  همگرا باشد(فرض خلف). چون
همگرا باشد(فرض خلف). چون داریم:
داریم: 
 داریم:
داریم: 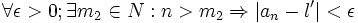
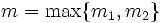 ، در این صورت برای هر n>m داریم
، در این صورت برای هر n>m داریم  و
و  که این دو باهم ایجاب میکنند:
که این دو باهم ایجاب میکنند: 
 که در این صورت خواهیم داشت:
که در این صورت خواهیم داشت:

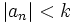


 ممکن است در این نامساوی صدق نکنند پس قرار میدهیم:
ممکن است در این نامساوی صدق نکنند پس قرار میدهیم: 
 ، نشان میدهیم
، نشان میدهیم . فرض میکنیم
. فرض میکنیم (فرض خلف). در این صورت چون دنباله به L همگرا است بنا به تعریف داریم:
(فرض خلف). در این صورت چون دنباله به L همگرا است بنا به تعریف داریم: 
 خواهیم داشت:
خواهیم داشت: 
 ، جملات دنباله از شمارهای به بعد با L همعلامت میباشند.
، جملات دنباله از شمارهای به بعد با L همعلامت میباشند.  در این صورت برای هر n>m داریم:
در این صورت برای هر n>m داریم: 
 و لذا در این حالت حکم برقرار است. حالت L<0 نیز به طریق مشابه اثبات میشود.
و لذا در این حالت حکم برقرار است. حالت L<0 نیز به طریق مشابه اثبات میشود. 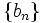 دو دنباله باشند که به ترتیب به
دو دنباله باشند که به ترتیب به  و
و 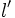 همگرا میباشند آنگاه:
همگرا میباشند آنگاه: 


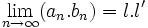



 و
و 


 آنگاه
آنگاه 
 در این صورت چون برای هر n طبیعی داریم
در این صورت چون برای هر n طبیعی داریم  پس بنا به قضیه 3، حد
پس بنا به قضیه 3، حد  نامنفی است پس داریم:
نامنفی است پس داریم: 
 و
و  واگرا میباشند.
واگرا میباشند.  نیز همگرا است که این تناقض است. پس فرض خلف باشد و
نیز همگرا است که این تناقض است. پس فرض خلف باشد و  سه دنباله باشند به طوری که برای هر n طبیعی، داشته باشیم
سه دنباله باشند به طوری که برای هر n طبیعی، داشته باشیم 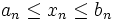 و نیز
و نیز  آنگاه:
آنگاه:

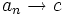 داریم:
داریم: 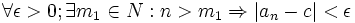
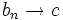 داریم:
داریم: 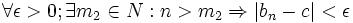
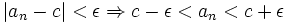
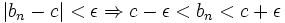
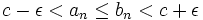
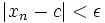 که این نشان میدهد:
که این نشان میدهد: 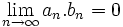
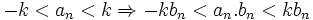
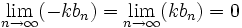 پس بنا بر قضیه ساندویچ داریم:
پس بنا بر قضیه ساندویچ داریم: 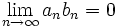
 زیرمجموعهای ناتهی از اعداد حقیقی و کراندار است بنابر تمامیت اعداد حقیقی دارای کوچکترین کران بالا یا سوپریمم است. قرار میدهیم:
زیرمجموعهای ناتهی از اعداد حقیقی و کراندار است بنابر تمامیت اعداد حقیقی دارای کوچکترین کران بالا یا سوپریمم است. قرار میدهیم:  به عبارت دیگر فرض میکنیم c کوچکترین کران بالای دنباله
به عبارت دیگر فرض میکنیم c کوچکترین کران بالای دنباله  به ازای عدد طبیعی N وجود دارد که
به ازای عدد طبیعی N وجود دارد که  . پس برای هرε>0 دلخواه بازه
. پس برای هرε>0 دلخواه بازه  شامل جملهای از
شامل جملهای از  و این نشان میدهد:
و این نشان میدهد: 


 به چهارتایی مرتب
به چهارتایی مرتب  . جبر کواترنیونها را
. جبر کواترنیونها را  با دوبار استفاده از
با دوبار استفاده از  از مبدا صفحه xy پرتاب میشود. همچنین فرض میکنیم پرتابه در ربع اول حرکت میکند و مقدار سرعت اولیه
از مبدا صفحه xy پرتاب میشود. همچنین فرض میکنیم پرتابه در ربع اول حرکت میکند و مقدار سرعت اولیه  است و بردار سرعت با محور xهای مثبت زاویه
است و بردار سرعت با محور xهای مثبت زاویه 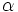 میسازد. در هر لحظه t ،
میسازد. در هر لحظه t ،  ، مکان پرتابه با جفت مختصات
، مکان پرتابه با جفت مختصات  . مشخص میشود. بنابراین پس از ساده کردن یک سری از معادلات به روابط زیر دست مییابیم که مکان ذره t ثانیه پس از پرتاب برای ما مشخص میسازد:
. مشخص میشود. بنابراین پس از ساده کردن یک سری از معادلات به روابط زیر دست مییابیم که مکان ذره t ثانیه پس از پرتاب برای ما مشخص میسازد: 
 در فضا مشخص باشد برای این کار طول
در فضا مشخص باشد برای این کار طول  را مییابیم که در اینصورت داریم:
را مییابیم که در اینصورت داریم:
 را بهم وصل میکند متوسط مختصات
را بهم وصل میکند متوسط مختصات  بگذرد و موازی با بردار
بگذرد و موازی با بردار  باشد. پس L مجموعه نقاطی است مانند
باشد. پس L مجموعه نقاطی است مانند  به قسمی که بردار
به قسمی که بردار  با V موازی است یعنی P بر L واقع است اگر و تنها اگر به ازای عددی مانند t داشته باشیم:
با V موازی است یعنی P بر L واقع است اگر و تنها اگر به ازای عددی مانند t داشته باشیم:  این معادلات را پس از ساده کردن بصورت معادلات پارامتری متعارف خط L درست مییابیم که عبارتاند از:
این معادلات را پس از ساده کردن بصورت معادلات پارامتری متعارف خط L درست مییابیم که عبارتاند از: 
 تا
تا 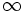 افزایش مییابد نقطه
افزایش مییابد نقطه  را میپیماید، P از نقطهای که در آن t=a تا نقطهای که در آن t=b بر روی یک پارهخط جابجا میشود.
را میپیماید، P از نقطهای که در آن t=a تا نقطهای که در آن t=b بر روی یک پارهخط جابجا میشود.  عمود است. پس M از مجموعه نقاطی مانند
عمود است. پس M از مجموعه نقاطی مانند 
 که بردارهای
که بردارهای  قائم بر دو صفحهاند توسط رابطه زیر حاصل میشود:
قائم بر دو صفحهاند توسط رابطه زیر حاصل میشود: 




 وبلاگ مهارت در ریاضیات
وبلاگ مهارت در ریاضیات